Moku升级实时计算并显示g(2)二阶关联函数及最新活动更新

摘要

Moku时间间隔与频率分析仪（TFA）功能进一步升级，在时间间隔测量精度与检测配置灵活性方面实现显著提升。全新版本支持实时计算并可视化显示g(2)二阶关联函数，为量子光学、单光子探测及相关前沿研究提供更高效、直观的测量手段。在本应用笔记中，我们将概述二阶关联函数及其物理意义。随后，我们将介绍如何使用Moku 时间间隔与频率分析仪进行配置并采集数据，说明如何使用其内置新增的分析功能来计算二阶关联函数。最后，我们将演示两种不同的计算方法，并展示两者结果具有良好一致性。

01

背景介绍

经典光源与量子光源具有广泛用途，既可覆盖量子光学、量子计算等量子领域，也可以应用于激光干涉测量等经典场景。光源通常可按其发射的统计特性进行分类，例如：相干光源、热光源、混沌光源或量子光。相干光源以激光为代表，其相位稳定，发射光子的数量涨落服从泊松统计。热光源（如白炽灯或恒星）则由大量彼此不相关的辐射体共同发光，往往呈现出突发形式的发射特征。量子光源（如压缩光或单光子发射体）会表现出“反聚束（anti-bunching）”效应：当刚探测到一个光子后，紧接着再探测到下一光子的概率最低。这是一种典型的量子效应，任何经典光源都无法产生。在量子应用中，表征光源的统计发射特性往往至关重要，因为这有助于验证所使用的是否为真正的量子光源。类似地，激光的精度通常会受限于由光子数目主导的泊松统计。评估光发射统计特性的一种方法，是使用二阶关联函数g(2)(τ)——这一指标在经典与量子光学中被广泛采用。在这篇应用说明中，我们介绍两种使用Moku测量g(2)(τ)的方法。自MokuOS 4.1起，时间间隔与频率分析仪内置了通过自卷积法实现g(2)(τ)实时计算功能。除此之外，我们还可以利用Moku时间间隔与频率分析仪采集含有时间戳的信号事件数据，然后通过全配对法在后处理阶段计算g(2)(τ)。我们将分别概述这两种方法，并使用Moku进行实验并记录带有时间戳的光子事件来加以验证。随后，我们将详细说明如何生成具有时延的直方图，并据此计算二阶关联函数，并将该结果与时间间隔与频率分析仪内置的g(2)(τ)计算功能进行对比。

02

什么是二阶关联函数

二阶关联函数g(2)(τ)用来回答一个问题：如果刚探测到一个光子事件，则过了τ之后再探测到下一个光子事件的概率，是比在“随机到达”的情况下更大还是更小。其中τ=0 处的值尤为重要，因为它可用于推断光源在同一时刻发射多个光子的可能性。例如：

若g(2)(0)>1，则光源倾向于成对发射光子。我们称为“聚束”，通常表明该光源具有热光源特征。举例来说，g(2)(τ=0)=2表示：在总测量时长T内，与“任意时间延迟τ”对应的平均符合计数相比，时间延迟接近0的符合事件（事件对）数量是前者的两倍。

若g(2)(0)<1，则光源倾向于以规律时间间隔发射光子，几乎不会在同一时刻发射超过一个光子。我们称为“反聚束”，是单光子光源所期望具备的重要特性。

若g(2)(0)=1，则发射光子之间不存在相关性（即到达时间彼此独立）。这常见于相干光源，例如激光。

这三种情况的仿真结果如下面图1所示。

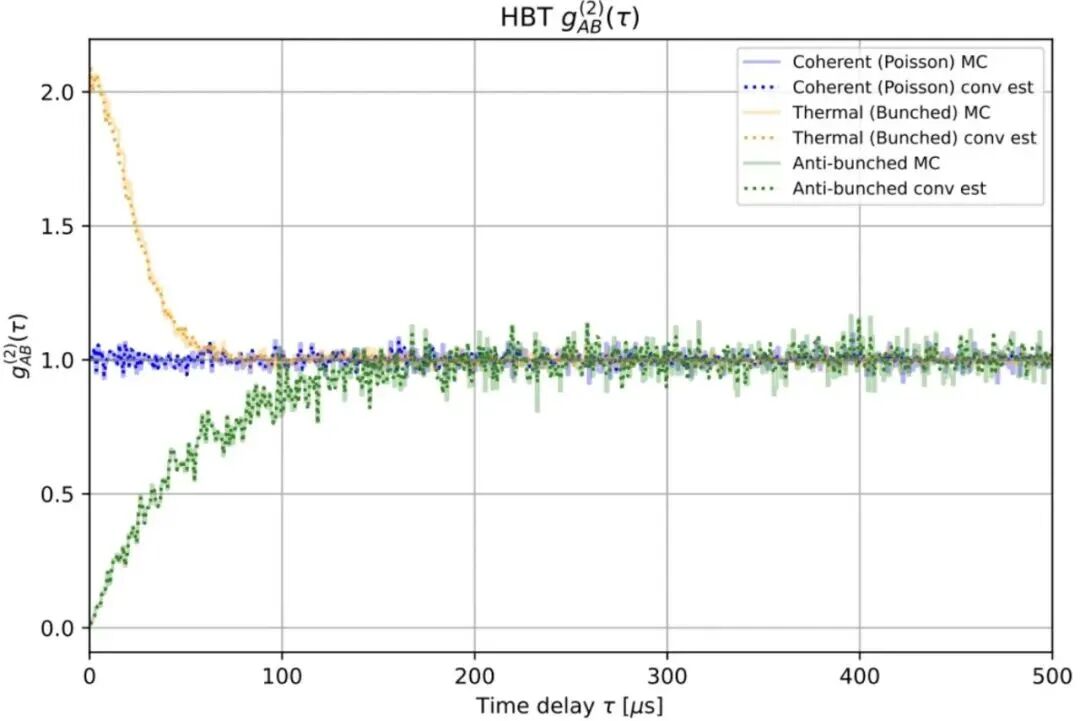图1.对泊松（随机）、聚束与反聚束三种情况进行的仿真结果如图所示。相干情形在整个时间跨距内始终保持在 1；而聚束与反聚束情形在τ=0 处分别趋近于 2 和 0。对于该图中的每一种情况，二阶关联函数均可以采用两种不同的方法计算得到。相关方法将在本应用笔记的后续章节中介绍。为演示如何使用并计算g(2)(τ)，我们先引入Hanbury–Brown–Twiss（HBT）效应。在HBT实验中（见图2），待测光源发出一串光子并进入一个50/50分束器，分束器将单个光子分配到两条光路中的任意一路。两个单光子探测器（被标记为“A”和“B”）分别监测两条光路中光子的到达情况。两臂之间的任意光程差都会导致两个探测器接收到光子的时间出现相对延迟（时间偏移）。当探测器记录到一次光子事件时，会产生一个电脉冲并将其送入时间间隔分析仪（TIA）。TIA的作用是对A、B两路的光子事件进行高精度时间戳标记与记录，用于后处理。正如我们将在下一节推导的那样，A与B两路事件之间的时间关联性决定了二阶关联函数的取值。

图2.典型的 Hanbury–Brown–Twiss（HBT）实验配置：对光电探测器 A 与 B 的输出信号进行测量。时间间隔分析仪用于记录从事件 A 到事件 B 的时间偏移（延迟）。

03

量化二阶关联函数和重合率

二阶关联函数g(2)(τ)可表示为光子探测计数的乘积在时间上的平均值：

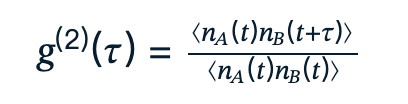
其中，nA(t)和 nB(t) 分别表示在时刻 t 与 t+τ时，探测器 A 与探测器 B 上的光子探测事件率。符号⋅ 内的量表示对时间取平均，即：

在建立了g(2)(τ)的定量定义之后，下面我们讨论如何求得nA(t) nB(t+τ)。这对应于时间平均后的符合率，也可以理解为在时刻t探测到一个光子事件、并在t+τ再探测到另一个光子事件的概率密度——且不论第一个事件来自哪一路探测器。这意味着，A路出现一次初始事件后，B路后续可能以级联形式依次出现第一个、第二个甚至第三个事件。在计算符合率时，这些情况都必须纳入统计。随后，将得到的各个τ值进行分箱处理并归一化，即可得到对nA(t) nB(t+τ)的预估。

04

测量时间延迟直方图

HBT实验的关键之一是时间间隔分析仪，它负责采集探测到的光子事件并生成时间间隔直方图。正如图3所示，Moku时间间隔与频率分析仪可针对HBT实验配置并进行测量。在该实验中，单光子探测器（SPDs）A与B分别接入Moku的输入1与输入2。时间间隔与频率分析仪可用于检测SPDs输出的脉冲信号，其中输入1作为事件检测的开始，输入2作为事件检测的终止。有关如何配置Moku以进行HBT测量的更多细节，请点击“阅读原文”参阅我们关于该部分内容的配置指南。

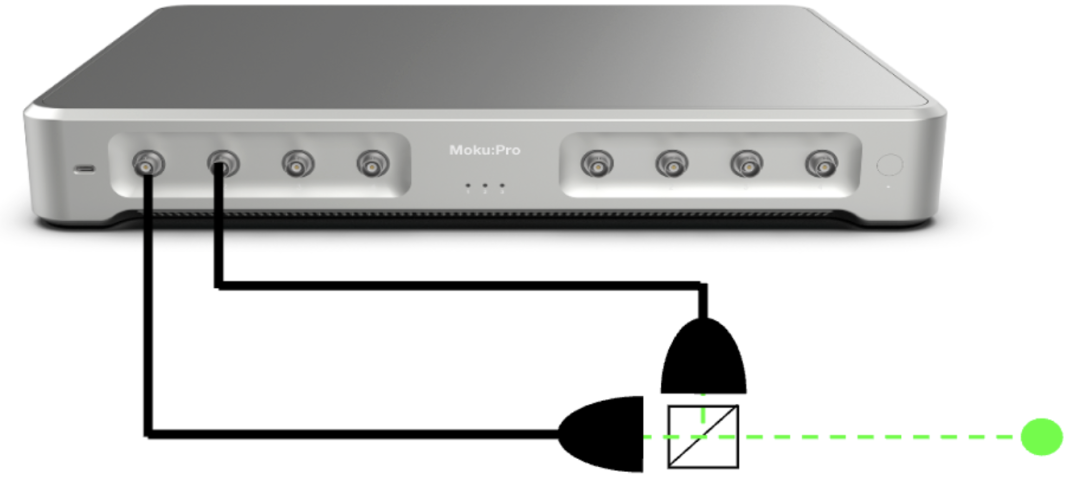
图3.使用 Moku 时间间隔与频率分析仪的HBT 测量配置，可生成延迟直方图并记录带时间戳的数据。在测量过程中，时间间隔与频率分析仪会记录连续发生的A、B事件之间的延迟时间，并据此实时构建被探测到的光子对的延迟数密度分布（即延迟直方图）。需要注意的是，时间间隔与频率分析仪实时生成的直方图仅统计第一阶段的符合事件，因此仍需进行一定的后处理才能计算出g(2)(τ)。值得一提的是，现在可以通过内置的自卷积过程，将时间间隔数据的分布转换为g(2)(τ)的近似结果；下一节将对此进行说明。这构成了Moku时间间隔与频率分析仪内置g(2)(τ)计算功能的基础。

05

数据分析

假设我们已经获得由时间间隔与频率分析仪采集到的时间间隔直方图。我们将该分布态势记为k(τ)，它记录的是：对某一路中的一个光子事件，在另一路中找到其后出现的第一个光子事件，并取这两次事件的到达时间差。用伪代码表示为：

正如上一节所述，k(τ)仅对应第一阶段延迟的概率密度函数。尽管k(τ)在形式上看起来与nA(t) nB(t+τ)相似，但它只包含一阶贡献，没有将因更长事件级联产生的光子纳入统计。举例而言，到达时刻为t+τ1+τ2或t+τ1+τ2+τ3的光子事件不会被计入。

因此，k(τ)通常不直接用于计算g(2)(τ)。相反，人们需要显式统计事件A与事件B之间的每一次符合计数，直至最大统计时间。用伪代码表示该过程为：

随后，将这些τ值进行分箱处理以生成直方图，并进行适当归一化，使得当某一延迟值下g(2)(τ)=1时表示该延迟值下不存在关联性。尽管该方法直观且直接了当，但其计算规模扩展性较差，因为需要将每一个事件A与每一个事件B进行比较，计算量为O(NA×NB)。当事件发生率较高时，这一运算量会迅速变得非常庞大。因此，这样很难在硬件上实现实时计算。

所以Moku时间间隔与频率分析仪采用了另一种替代方法来实时计算g(2)(τ)，该方法更利于发挥FPGA的性能优势。其核心是对k(τ)进行高阶自卷积，得到一组分布k(n)(τ)。其中k(n)(τ)表示：在一级联光子事件序列中，相对于初始触发事件，后续第n次光子事件出现在延迟τ处的概率密度。换言之，它对应于从初始光子事件到第n个后续光子事件之间的延迟分布。将所有阶次的贡献叠加后，得到在初始触发之后、延迟为τ处观测到光子事件的总概率密度G(τ)（不区分来自第几次后续光子事件），其与下式所示的无限求和成正比[1]：

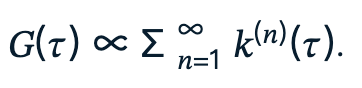
该求和关系式可以理解为对彼此互斥的多种路径取“逻辑或”：它表示在延迟τ处观测到一次光子事件，可能来自后续的第1次事件、或第2次、或第3次，以此类推。每一项对应一种相互独立的可能性；将它们相加即可得到延迟为τ时的总到达密度。因此，

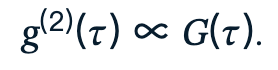
在下一节中，我们将以两种方式测量g(2)(τ)：第一种是记录事件时间戳并通过全配对法计算完整的成对统计结果；第二种是使用Moku内置的g(2)(τ)计算功能。

06

使用 Moku 时间间隔与频率分析仪模拟实验并验证 g(2)(τ)

为仿真泊松事件分布，我们使用Moku:Pro搭建了一套全数字电路实验系统。利用MiM -多仪器并行模式，我们将Moku的FPGA划分为四个仪器插槽，每个插槽分别部署实验所需的仪器功能。配置与连接示意图见图4。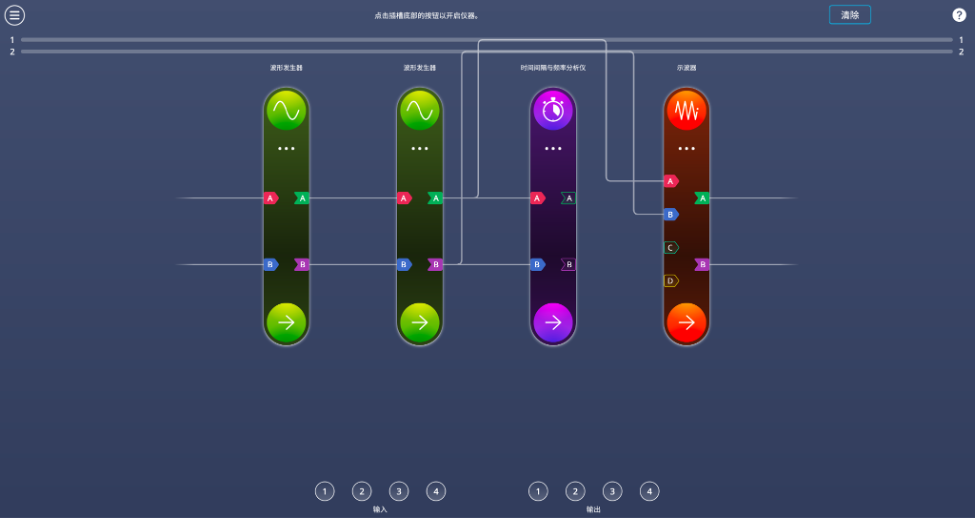图4.多仪器并行界面。第一个波形发生器充当“光子源”，并触发第二个波形发生器输出脉冲。脉冲信号被连接到Moku时间间隔与频率分析仪进行统计计算。示波器用于监测第二个波形发生器的输出。首先，我们配置第一个波形发生器，用于产生两路彼此不相关的噪声信号。在配置界面中，点击并打开输出A与输出B。将两路输出的波形类型设置为“噪声”，并将幅度设为1 Vpp。波形发生器的配置如图5所示。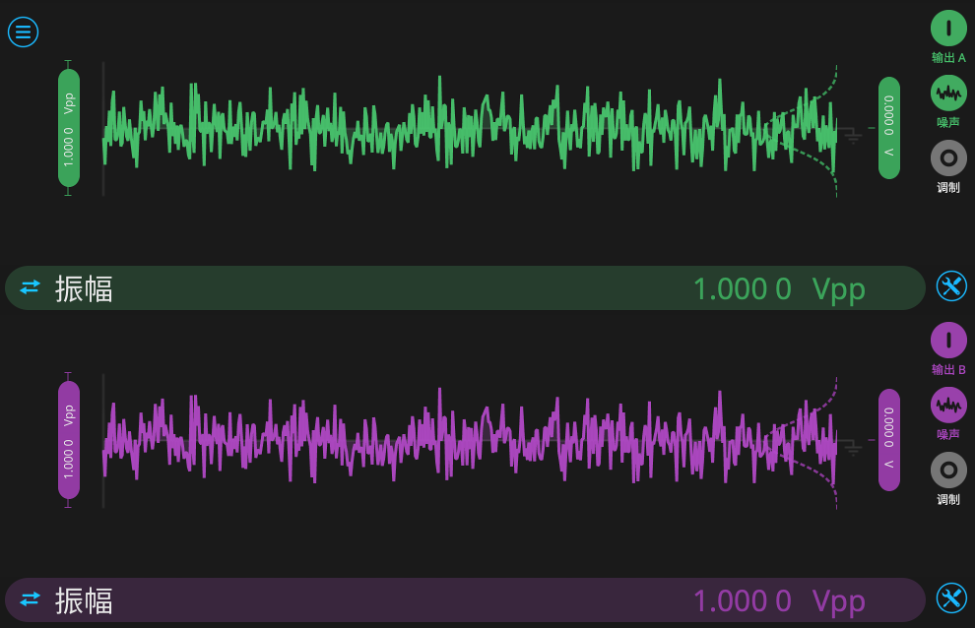图5. Moku 波形发生器配置。用于生成两路彼此不相关的噪声信号

其次，我们配置第二个波形发生器来模拟一对光电探测器。我们选择脉冲输出，频率设为10 MHz，脉冲宽度设为20 ns。随后启用N周期突发模式，并将触发阈值设为400 mV。每个通道分别由第一个波形发生器的一路噪声源来触发。通过这种方式，当输入信号达到设定电压阈值时，第二个波形发生器就会被触发并输出一个方波脉冲，从而在行为上模拟单光子探测器的输出。本例中阈值被设为400 mV，也可以调整该阈值，以改变“光子”事件的发生频率。第二个波形发生器的配置如图6所示。

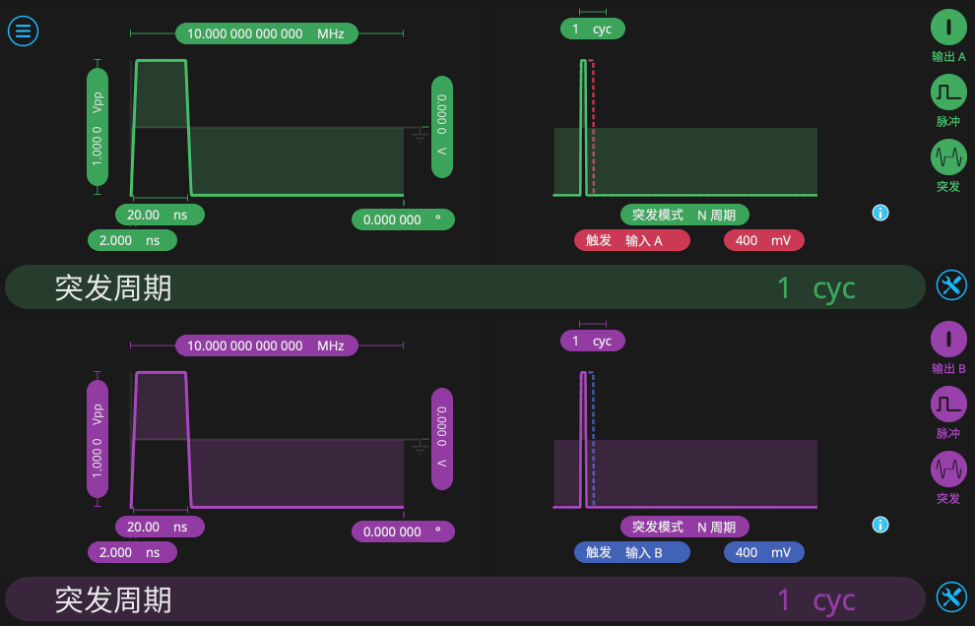图6.第二个波形发生器配置界面，两个通道被配置为输入的噪声信号到达设定阈值时，会触发并输出一个方波脉冲，以此来仿真单光子探测器。

然后，我们配置时间间隔与频率分析仪，用来检测在输入A和输入B通道上发生的“光子”事件。在事件配置选项卡中，将事件检测设置为上升沿触发，阈值设为0 V；随后测量从事件A开始到事件B结束的时间间隔。由于事件重复频率较高，我们采用窗口化采集模式进行测量，并将测量时间窗口设为100 ms，以获取足够多数量的信号事件。最后，我们在第四个仪器槽上部署示波器，用于观察第二个波形发生器的输出。完成所有仪器部署配置并启用波形发生器输出后，即可在示波器上看到如图7所示的波形：A、B两个通道上均应出现随机分布的“事件”脉冲信号，我们会发现有时两个脉冲信号会在时间上非常接近。

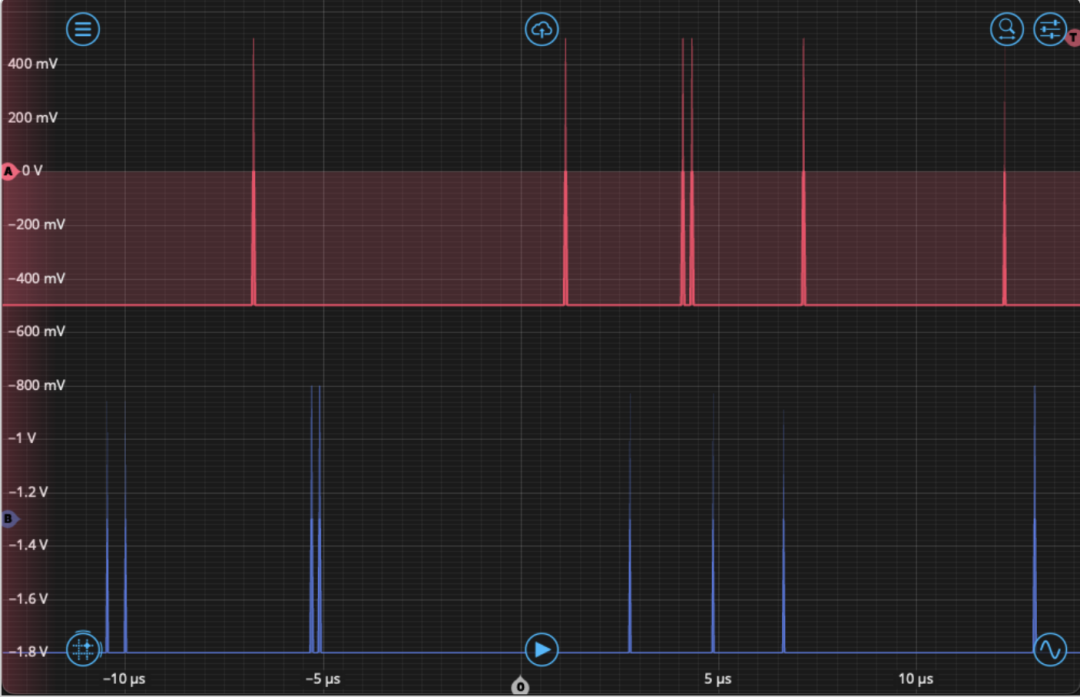
图7. 示波器显示界面，显示第二个波形发生器输出的“光子”事件脉冲，模拟部分商用单光子探测器所使用的TTL输出信号类型。打开时间间隔与频率分析仪的仪器界面，我们同样会看到这些事件在直方图中逐渐累积。正如上一节所述，该直方图仅反映最近相邻事件之间的时间间隔，并未包含二阶或三阶等更高阶级联事件的贡献。点击名为“间隔直方图”的按钮即可切换显示，以此查看仪器内置的g(2)(τ)计算结果。我们在图8中并排对比显示这两种结果。由于二阶关联函数是对直方图进行自卷积得到的，其曲线形态会有明显差异；其数值整体在1附近波动，表明事件A与事件B之间不存在关联性——这也正是伪随机分布理应得到的预期结果。

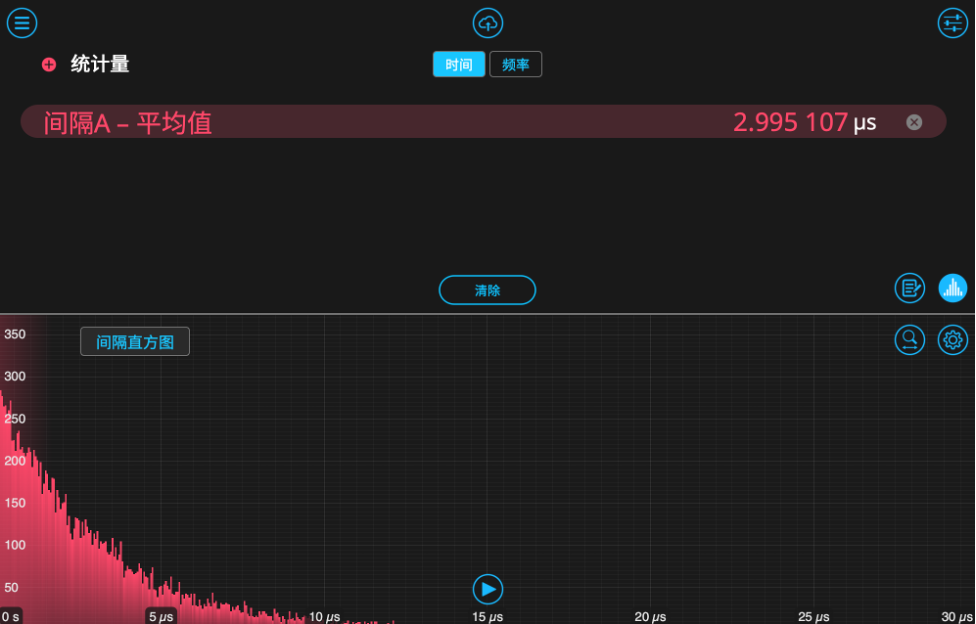
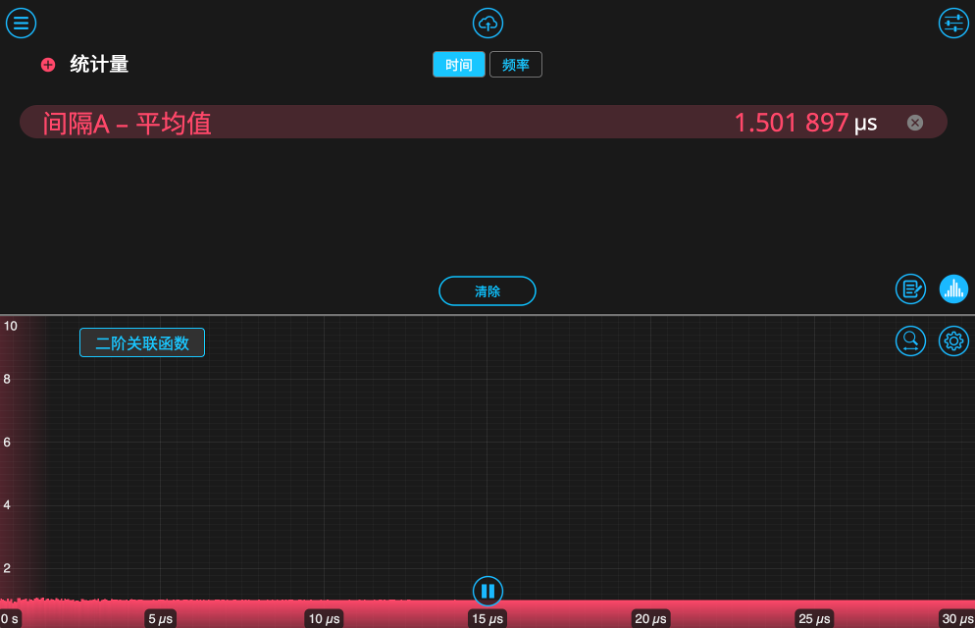图8.上：实时更新显示的直方图，呈现从事件A到事件B的时间间隔分布。下：g(2)(τ)曲线在1附近保持稳定，表明事件之间不相关性。

07

通过Python读取时间戳数据计算g(2)(τ)

为验证两种方法的一致性，下面我们将使用时间间隔与频率分析仪记录的时间戳数据来估算g(2)(τ)。

第一步在导入常规的模块包之后，将记录数据分别读入两个数组A_times和B_times。随后，我们对每个事件A寻找其后出现的下一个事件B，从而得到一阶时间间隔信息——这与Moku时间间隔与频率分析仪绘制的直方图结果一致。有了时间戳数据与直方图信息后，我们即可按上一节所述的方法计算g(2)(τ)。第一种方法如图9所示：对A_times中的每个事件，搜索B_times中所有发生在其后的事件，并计算相应的时间延迟。这些延迟值随后进行分箱处理并作适当归一化。

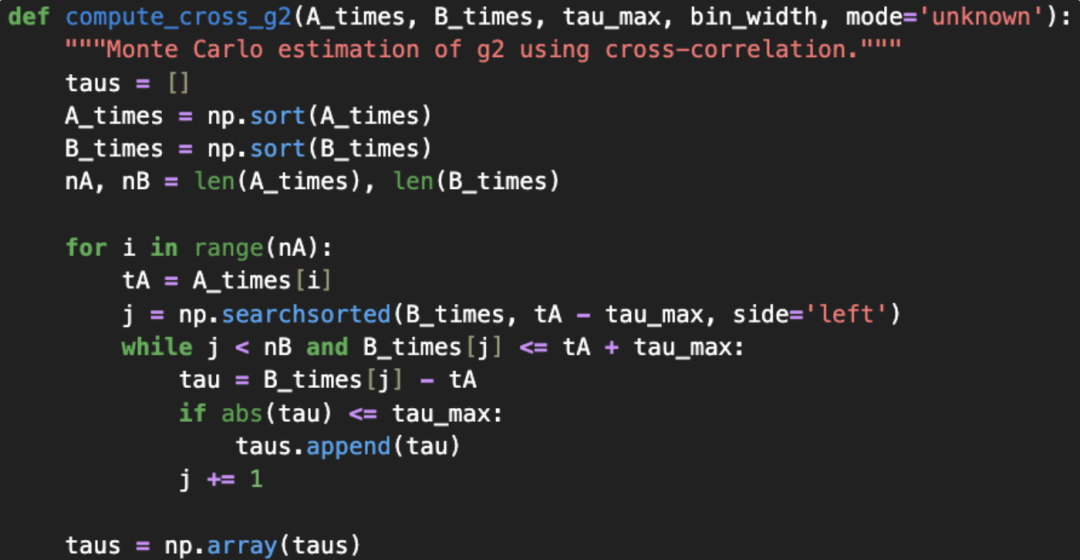
图9：通过手动计算所有时间延迟来求取g(2)(τ)，即全配对方法。第二种方法中，我们对一阶事件直方图进行自卷积，可得到一个与前述定义的时间平均符合率成正比的量。为此，我们先配置时间间隔与频率分析仪，并通过get_data()函数获取直方图数据；该函数会返回时间分箱列表，以及对应每个分箱计算得到的g(2)(τ)数值。相关代码如图10所示。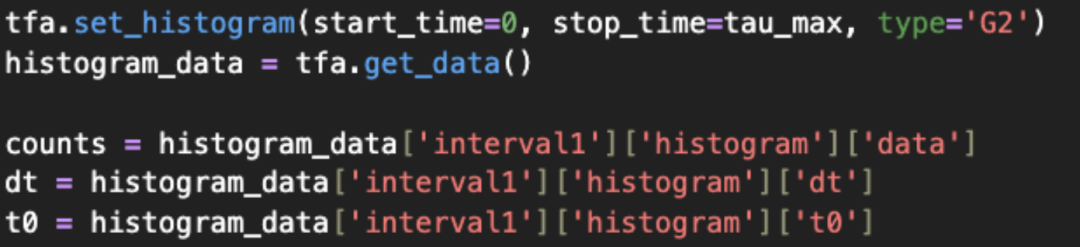图10：使用Python直接从Moku设备获取g(2)(τ)数据。接下来，我们将两种方法的结果进行对比：把完整的全配对计算结果与Moku设备内部计算得到的曲线并排绘制。对比结果如图11所示。两种方法计算结果良好吻合，在整个时间范围内均得到接近1的g(2)(τ)值——这正是两路互不相关信号所应呈现的预期结果。

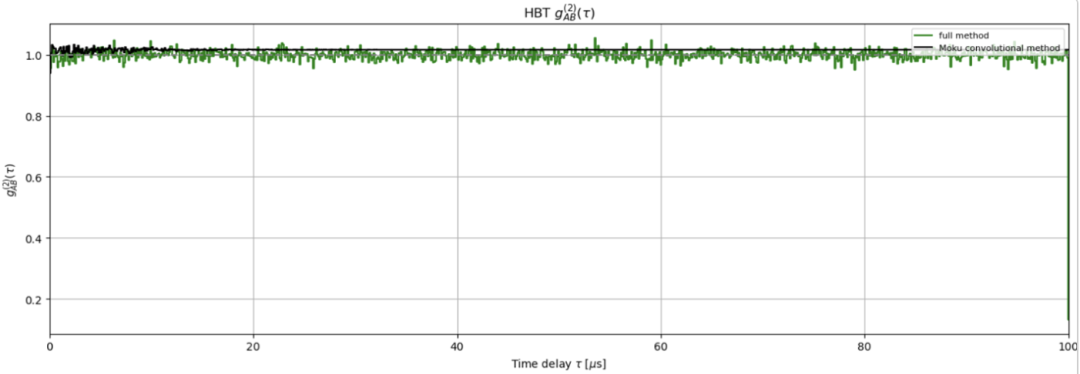
图11：绘制从Moku采集的g(2)(τ)数据曲线。该结果分别采用全配对方法与时间间隔与频率分析仪的卷积近似两种方式得到。将两者绘制在同一时间轴上可见良好一致性。

由于两种计算路径不同，卷积法与成全配对法在g(2)(τ)上可能会出现细微差异，尤其是在τ≈0处附近。卷积法使用由Moku得到的、经过分箱处理的直方图数据进行计算；而全配对法则对所有事件对组合进行显式计算。

这两种方法在数学上都是计算二阶关联函数的有效途径。对于大多数应用而言，它们会给出等效的结果。但也需要注意，在某些边界条件或特定类型探测器的配置下，两种方法之间可能会出现轻微差别。

总结

二阶关联函数是一种用于评估光源的时间动力学的强有力工具；在量子光学应用中更是至关重要，其应用范围覆盖从加密通信到光子计算等方向。

Moku时间间隔与频率分析仪具备亚皮秒的数字分辨率且无死时间，用于精确测量事件之间的时间间隔。不仅支持单一界面对光子、频率和事件进行计数，还可以执行抖动分析和记录高分辨率原始事件时间戳，最新升级版本增加了实时计算和显示g(2)(τ)功能。

在本文中，我们使用Moku时间间隔与频率分析仪通过两种方法计算了二阶关联函数g(2)(τ)。第一种方法是利用时间间隔与频率分析仪内置的g(2)(τ)实时计算功能，通过卷积法生成该结果。第二种方法则演示了如何以精确时间分辨率采集带时间戳的光子事件，并使用Python进行计算分析，通过全配对方法计算g(2)(τ)。将两种结果并排绘制后，我们验证了它们之间具有良好一致性。

无论是研究相干激光，还是单光子发射源，熟悉这两种g(2)(τ)的计算方法将有效帮助用户识别相对于理想行为的偏差，并对光源性能进行高效量化评估。

市场活动预告

Moku是由Liquid Instruments基于FPGA技术开发的多功能测试测量平台，结合高带宽模数转换器和数模转换器，实现信号生成、调节控制及测试分析等16+种仪器功能。最新高性能型号Moku:Delta支持同时部署运行任意波形发生器、激光锁频/稳频器、锁相放大器、时间间隔与频率分析仪等高达8种仪器功能，不仅满足激光稳频与功率稳定要求，还可应对微弱信号的解调检测、光子计数，以及原子阵列的二维排布与精确寻址等多重测试测量需求，极大缓解了量子实验系统的复杂性。单台设备可配置超过二十亿种自定义测试测量方案，最大限度地满足量子实验定制化需求。